| |
| |
Hier nun die Lösung des Rätsels: |
| |
|
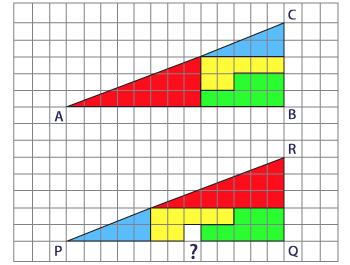
Beachte die beiden folgenden Abbildungen ABC
und PQR. Die Region in ihnen ist rot, blau, grün und gelb gefärbt. Ihre
entsprechenden Formen und Flächen sind gleich. |
| |
 |
| |
|
Die Position der grünen Form ist bei beiden
gleich. Die anderen drei Formen (rot, blau und gelb gefärbt) sind in der
Abbildung unten verschoben. In dieser Konfiguration siehst Du, das ein
zusätzliches Quadrat in Weiß angezeigt wird. Betrachte die Seite jedes
kleinen Quadrats in den Figuren als eine Einheit. |
| |
|
Die beiden Seiten mit dem rechten Winkel in
den beiden Figuren sind gleich lang. Das heißt, die Basen bestehen aus
13 Einheiten, während die Höhen aus 5 Einheiten bestehen. Woher kam dann
der Unterschied? |
|
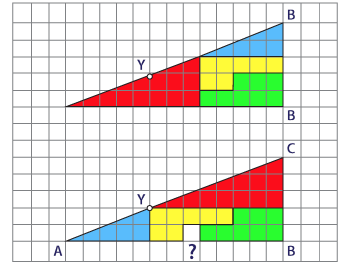
Markieren wir einen Punkt auf beiden Figuren
an derselben Stelle wie gezeigt. |
|
 |
| |
|
Wenn Du es genau bemerkst, befindet sich Y in
der Abbildung unten auf einer Höhe von 2 Einheiten von der Basis. Die
Höhe des gleichen Y in der Abbildung oben beträgt weniger als 2
Einheiten! Dies impliziert, dass AC und PR nicht gleich lang sind. Hier
liegt das Paradoxon. Die beiden Figuren oben und unten sind überhaupt
keine Dreiecke !!! Die Linien von AC und PR sind tatsächlich verbogen.
Was ist verblüffend an diesem Rätsel? Intuitiv halten wir die beiden
Figuren für ein Dreieck bzw. für ein gleich großes Dreieck mit Lücke,
obwohl uns der Verstand sagt, dass die beiden Flächen gleich sein
müssten. Der Zuschauer wird einfach nur optisch getäuscht: Die
Gesamtgebilde sind keine Dreiecke, sondern tatsächlich Vierecke. Der
Trick liegt darin, dass das rote und blaue Dreieck nur scheinbar ähnlich
im geometrischen Sinn sind. Ihre Winkel sind in Wirklichkeit
verschieden. |
| |
 |
| |
|
Die beiden Gesamtdreiecke haben folglich nicht
drei, sondern vier Ecken; davon ist eine Ecke allerdings kaum sichtbar.
Sie befindet sich aber dennoch am Übergang vom roten zum blauen Dreieck.
Die oberen Kanten des roten und blauen Dreiecks erscheinen im
angeblichen Gesamtdreieck als eine lange Gerade, als Hypotenuse des
angeblichen Gesamtdreiecks. In Wirklichkeit hat die scheinbare lange
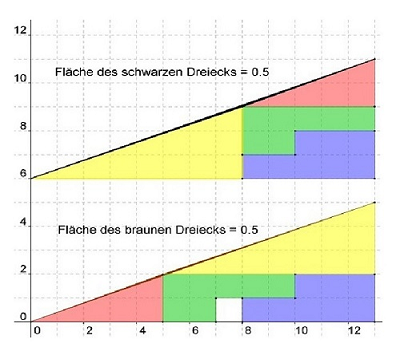
Gerade einen Knick, das ist die vierte Ecke. <br>Das scheinbare obere
Gesamtdreieck ist ein konkaves (eingedrücktes) Viereck, und das
scheinbare untere Gesamtdreieck ein konvexes (aufgebogenes) Viereck. Die
Flächeninhalte dieser beiden Vierecke unterscheiden sich um 1 cm². Dies
entspricht dem fehlenden Quadrat. An dem unterem Bild ist das vielleicht
leichter zu erkennen. |
| |
 |
| |
|
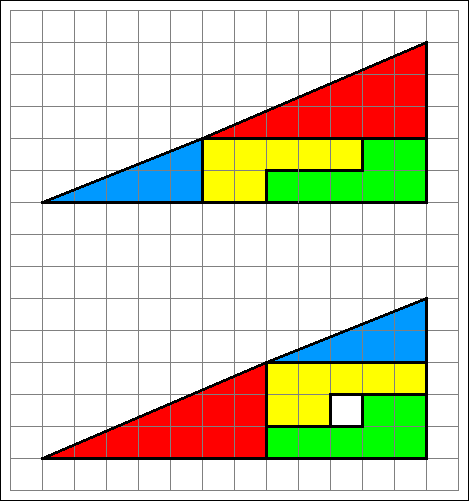
Und hier noch zwei weitere Beispiele: |
| |
 |
 |
| |
|
|
| |
| |
|
©_Andreas_Rybacki |





