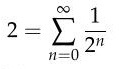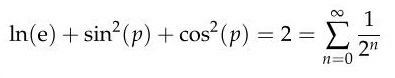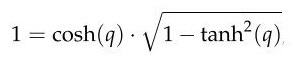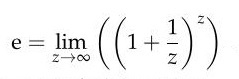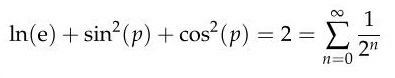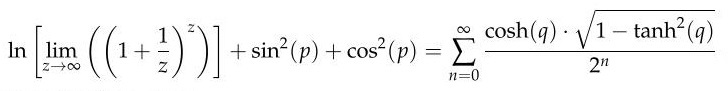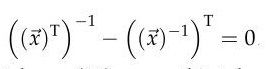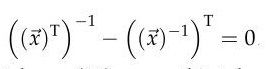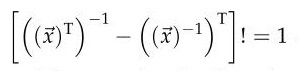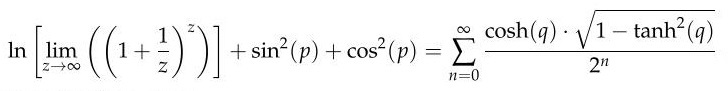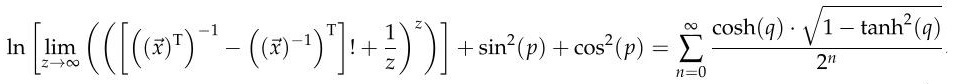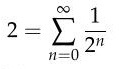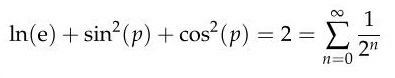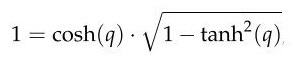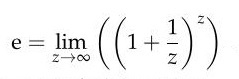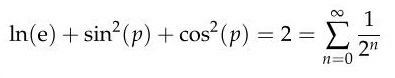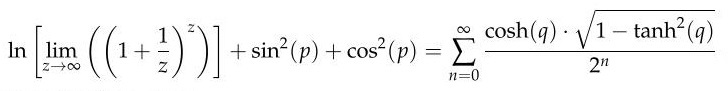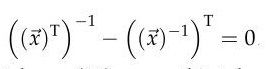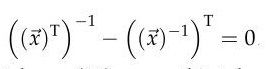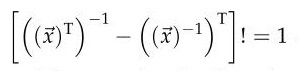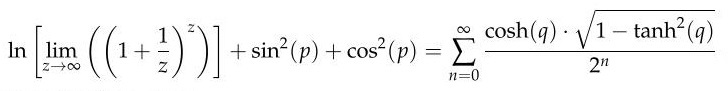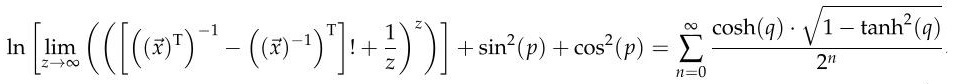| |
|
|
Erste Lektion in angewandter Mathematik |
|
|
|
Jedem angehenden Ingenieur wird schon zu
Beginn beigebracht die Summe von zwei Größen nicht etwa in der Form |
|
|
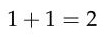 |
|
|
|
Diese Form ist banal und zeugt von
schlechtem Stil. Schon Anfangssemester wissen nämlich: |
|
|
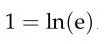 |
|
|
|
und weiterhin |
|
|
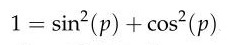 |
|
|
|
Außerdem ist für den kundigen Leser
offensichtlich, dass |
|
|
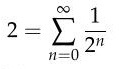 |
|
|
|
Daher kann |
|
|
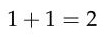 |
|
|
|
viel wissenschaftlicher ausgedrückt werden
in der Form |
|
|
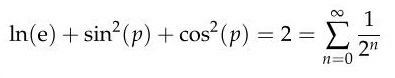 |
|
|
|
Weiteres ist sofort einzusehen: |
|
|
6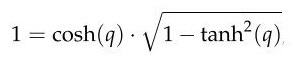 |
|
|
|
und |
|
|
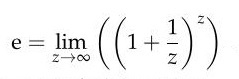 |
|
|
|
Deshalb kann nun |
|
|
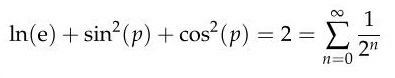 |
|
|
|
zu folgender, leicht verständlicher Form vereinfacht werden: |
|
|
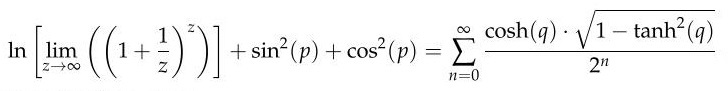 |
|
|
|
Wenn wir berücksichtigen, dass |
|
|
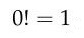 |
|
|
|
und wir uns daran erinnern, dass die Inverse der transponierten
Matrix die Transponierte der Inversen ist, können wir durch die
Einschränkung auf einen eindimensionalen Raum eine weitere Vereinfachung
durch die Einführung des Vektors x erzielen, wobei |
|
|
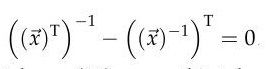 |
|
|
|
Verbinden wir die Gleichung |
|
|
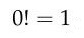 |
|
|
|
mit der Gleichung |
|
|
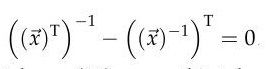 |
|
|
|
so ergibt sich Logischerweise |
|
|
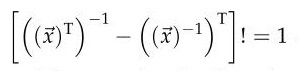 |
|
|
|
Eingesetzt in der Gleichung |
|
|
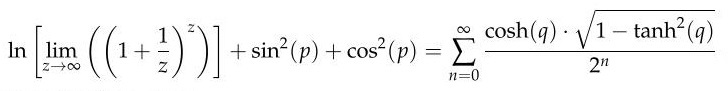 |
|
|
|
reduziert sich unser Ausdruck in der Form |
|
|
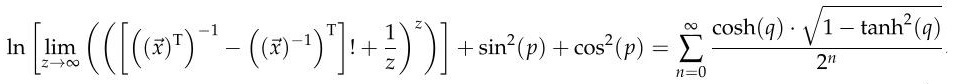 |
|
|
|
Spätestens jetzt ist offensichtlich, dass
die Gleichung viel klarer und leichter zu verstehen ist als |
|
|
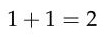 |
|
|
|
Es gibt noch eine Reihe anderer Verfahren,
um die Gleichung |
|
|
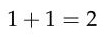 |
|
|
|
zu vereinfachen. Diese werden jedoch erst
behandelt, wenn der angehende Ingenieur die hier angewandten einfachen
Prinzipien verstanden hat. |
|
|
| |
 |
 |
 |
| |
| |
|
|